Teoria e cálculos
Objetivo Geral: A equipe deve elabora, projetar e construir uma catapulta seguindo o modelo trebuchet, com a função de lançar um projétil, bola de golf, e atingir o máximo alcance.
Objetivo especifico: Construir uma catapulta, utilizando em sua estrutura palitos de churrasco, cola e polímeros; O dispositivo deverá medir 500~700 milímetros de altura, 400~500 de largura X comprimento; A catapulta possuirá um estrutura capaz de suportar um contrapeso de 1 quilograma, integrado ao sistema de lançamento com cabos de cadarço de tênis ligados a um suporte de couro; Deverá conter também um sistema de elevação, feito com roldanas de nylon e cadarços de sapato.
Para a construção da catapulta foi necessário explorar
algumas vertentes da física mecânica estudadas durante o curso, dentre elas o
movimento oblíquo relacionado ao lançamento do projétil, a teoria de
conservação de energia, o momento de força e o momento angular, popularmente conhecido como
torque.
O lançamento da bolinha pela catapulta é um movimento em duas dimensões, tido como um Movimento Oblíquo de forma que há duas componentes da velocidade, uma horizontal, representada como um vetor v, que obedece um movimento uniforme e outra vertical, um vetor y, que segue a equação do movimento em queda livre [1]. Dessa forma, o móvel inicia a trajetória com uma velocidade inicial partindo da origem do plano cartesiano e definida por um determinado ângulo, logo o vetor velocidade do objeto é a resultante da velocidade horizontal e vertical da partida pelo braço da catapulta.

Figura 1:Movimento Oblíquo de um projétil. Disponível em:
https://vamosestudarfisica.com/lancamento-o-que-e-lancamento-obliquo/
 |
| Equação 1: Fonte própria. |
Pode-se analisar que a gravidade é uma força constante na direção
vertical, para baixo, portanto a componente horizontal da aceleração é nula,
enquanto a componente vertical será -gt em qualquer posição [1] , logo aplicando
conceitos da cinemática as fórmulas empregadas nesta situação são:
 |
| Equação 2: Componentes da velocidade. Fonte própria |
 |
| Equação 3: Componentes da posição. Fonte própria |
Onde v é velocidade (m/s), g é
a constante gravitacional (9,79m/s2),
t é tempo (s) e x e y são as posições
no eixo cartesiano (m).
Para calcular o alcance primeiro utiliza-se a
equação da componente “y” da velocidade ( Equação 4) para descobrir o tempo de voo da bola
de golfe, igualando ela a 0, visto que a velocidade nesse instante é zero, então encontra-se o intervalo de tempo “t” necessário para ela atingir a altura máxima.
Com isso, multiplicando esse valor por dois (2t), temos o intervalo de tempo
total da bola no ar. Logo,
 |
| Equação 4: Tempo alcance máximo. Fonte própria. |
Depois, substituímos esse tempo e as equações 2 (componentes
da velocidade) na função da posição da componente “x” para encontrar, a partir
desses valores, o alcance máximo do lançamento, assim, encontramos a seguinte
equação:
 |
| Equação 5: Alcance máximo. Fonte própria. |
Onde v0 é a velocidade inicial; θ o angulo de lançamento e g a gravidade local.
Assim, analisamos que ∆x é uma função que depende da velocidade inicial, do valor da
gravidade e do ângulo de lançamento. Com o valor do ângulo que queremos variar
monta-se a equação 6 e é
possível encontrar o ângulo para o alcance máximo igualando a primeira derivada
dessa função a 0, logo:
 |
| Equação 6. Fonte própria. |
 |
| Equação 7: Derivada da equação 6. Fonte própria. |
Assim, o ângulo que dará o alcance máximo será o seu seno,
seja igual ao seu cosseno, ou seja, 45 graus.
Substituindo o valor do seno e cosseno de 45 graus na
equação 5, é possível encontrar a equação que dará , então, o alcance máximo
:
 |
| Equação 8: Alcance Máximo. Fonte própria. |
Logo, substituindo os dados coletados pela equipe na equação 8, g= 9,79m/s
2 e v0= 3,33488 m/s (encontrada através da teoria de Torque adiante), encontramos que o alcance (
∆x) é 1,13 m.
Outro conceito importante é o Princípio da Conservação de Energia, o qual diz que toda perda de alguma
forma de energia é compensada pelo aparecimento do mesmo valor de energia, em
outra forma. Então, quanto ao lançamento do objeto pela catapulta, duas
energias são consideradas, a Energia cinética e a Energia Potencial Gravitacional,
a primeira associada à energia que um corpo possui em decorrência de seu movimento
e a última ao estado de separação entre dois corpos que se atraem mutuamente
através gravidade [2]. Dessa forma, no instante inicial, a única energia que há no sistema é a potencial
gravitacional da anilha, que se encontra erguida e acumulando essa energia para
arremessar a bola de golfe, logo, essa energia será :
 |
| Equação 9: Energia inicial (potencial). Fonte própria. |
Onde, considera-se E
0 a energia potencial inicial, m a massa da anilha (1,161 kg), g a gravidade (9,79 m/s
2) e h a altura da anilha em relação ao solo (0,545 m). Dessa forma essa energia será igual a 6,19 J, porém, no instante do lançamento a igualdade será:
 |
| Equação 10: Energia no lançamento. Fonte própria. |
Sendo m1 a massa da anilha, h0 a
altura inicial da anilha, m2 a massa da bola de golfe, h1
a altura em que a bola é lançada e v será a velocidade de lançamento da bola de
golfe.
Ademais, quanto à estrutura da catapulta existe o Torque, ou o momento de força, o qual define-se
como a força que faz um objeto adquirir aceleração angular, girando em torno de
um eixo [3]. Essa força é relacionada ao movimento resultante do braço da catapulta, de maneira que a força aplicada e a distância entre seu eixo de rotação irá interferir na rotação. Então, para que haja a movimentação do sistema esse movimento
deve ser diferente de zero, chamado de torque dinâmico.
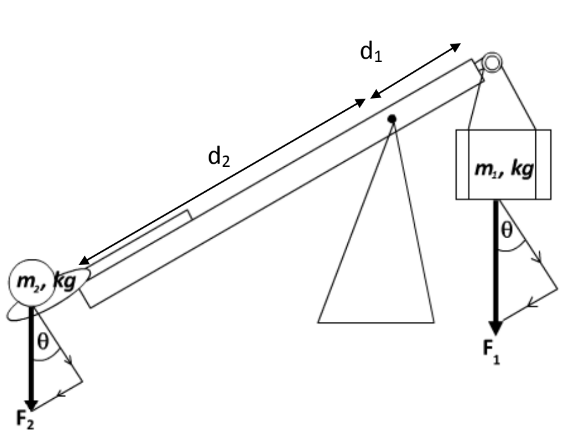
Figura 2: Ilustração teórica. Disponível em: |
Analisando as forças atuantes na catapulta (Figura 2), percebemos que a
força ideal, ou seja, a que daria maior torque, é quando esta se encontra perpendicular
ao braço da catapulta. Para isso usaríamos a seguinte fórmula:
 |
| Equação 11: Torque. Fonte própria |
theta
Onde considera-se r , como o d1 ou d2 na figura 2, que é a distância do ponto fixo ao contra peso e ao projétil respectivamente; e F é a força que atua no contrapeso e no projétil.
Pela fórmula também fica claro que se aumentarmos a distância entre contrapeso e ponto fixo (r) aumentaríamos o torque, o mesmo ocorreria se usássemos a força perpendicular ao braço [4]. Entretanto, há pouco a se fazer para garantir que a força esteja perpendicular ao braço a todo momento, além de ser muito difícil aferir o ângulo formado entre a força peso ( F1 e F2 ) e suas decompostas. Devido a isso iremos usar somente
as forças peso F1 e F2.
Sabendo que o somatório
do Torque nada mais é que o torque total, ou seja, o Torque no contrapeso
menos o Torque no projétil [1], logo escrevemos da seguinte forma:
Equação 12: Somatório de torque. Fonte própria.
Vale ressaltar que deve diminuir o
torque no contrapeso pelo do projétil, pois o sistema é uma alavanca. Além disso, como
estamos aplicando torque a um móvel podemos relacioná-lo com Aceleração Angular do sistema, ou seja, a aceleração que em que o ângulo variará
usando as seguintes relações:
Equação 13: Torque e Momento de Inércia. Fonte própria.
Onde I é o
momento de inércia e α a aceleração angular.
Para aplicar tal conhecimento é necessário realizar o somatório do momento de inércia (Equação 9), pois diferentemente do torque, o qual subtrai os termos, este não gera movimento [4].
Equação 14: Somatório do Momento de Inércia. Fonte própria.
Sabendo
disso podemos isolar o α, utilizando as relações anteriores, para então aplicar na fórmula a seguir para encontrarmos a velocidade angular na saída do
projétil:
Equação 15: Velocidade Angular. Fonte própria.
Onde, W = Velocidade angular final (rads-1), Wo= Velocidade angular inicial (rads-1), α= Aceleração angular (rads-2) e θ= Deslocamento Angular (rads).
Sabendo que o projétil parte do repouso e que a sua posição inicial será considerada como 0º, então Wo equivale à zero. Logo, determina-se a velocidade angular (W), em uma certa variação angular (V), a partir da equação 16:
Equação 16: Velocidade Linear. Fonte própria.
Após isso, teremos a velocidade de saída do projétil, e consequentemente o alcance esperado. Através dos conhecimentos aqui apresentados, as nossas estimativas são:
g=
9,79m/s2 ; m1=1,16190
Kg; m2=0,0467 Kg; d1= 0,15m;
d2= 0,4m; h0= 0,545m; h1= 0m.
1- Utilizando a Equação 12: ∑τ= 2,0551168 N;
2- Utilizando a Equação 14: ∑I= 0,041762 kg·m²;
3- Utilizando a Equação 13: α= 49,21021024 rads-2;
4- Utilizando a Equação 15: W= 8,789768488 rad/s;
5- Utilizando a Equação 16: V= 3,515907395 m/s2.
|
Modelo 3D
Por fim, foi realizado uma modelagem 3D em um CAD, SolidWorks, a fim de visualizar e verificar as dimensões escolhidas pela equipe. Vale ressaltar que se trata de um desenho teórico, que funcionará de base para a construção do projeto.
Figura 3: Catapulta Trebuchet em modelagem 3D. Fonte própria.
Figura 4: Vista superior da estrutura, com cotas. Fonte própria.
Figura 5: Perspectiva Isométrica da estrutura. Fonte própria.
Figura 6: Vista lateral da haste, com cotas. Fonte própria.
Figura 7: Vista lateral do compartimento para a anilha. Fonte própria.
Figura 8: Perspectiva isométrica do compartimento para a anilha. Fonte própria.
|
Referências:
[1] - HALLIDAY, David. Física para Cientistas e Engenheiros. Quinta Edição. Rio de Janeiro. LTC Editora. 2004. 368 Páginas.
[2] - CHAVES, Alaor; SAMPAIO, J.F. Física Básica: Mecânica. LTC Editora.
Rio de Janeiro,2012. 308 páginas;
[3] - Torque e momento angular. Disponível em: https://pt.khanacademy.org/science/physics/
torque-angular-momentum/torque-tutorial/a/torque. Acessado: 30/06/2018 às 22:00
hrs.
[4] - LUCAS, Stephen. Factors affecting the range of a Trebuchet. Disponível em: http://www.ucl.ac.uk/~zcapf71/Trebuchet%20coursework%20for%20website.pdf. 75 pág. Acessado em 06/07/2018.



























